Dijkstra算法
📌 简介
Dijkstra 算法是一种单源最短路径算法,用于计算从一个起点到图中其他所有顶点的最短路径。 适用于边权非负的图。
🧠 算法思想
创建一个集合S,从start开始每次都将当前计算出的距离集合S所有节点里路径最短的节点加入到集合S中,直到遍历完所有的点。Dijkstra最重要的一个思想就是第一次遍历到某个节点,将这个节点加入到S中,那么这个节点的最短路径就计算好了,后面一般不会再修改它(有些时候如果求的不是最短路径可能会修改)。
这是因为每次会选择距离集合S中所有节点里路径最短的那个节点加入到S中,Dijkstra需要图保证没有负边,因此加入到集合S的节点的路径只会越来越大。那么对于同一个节点来说,一旦它加入到S中,后面再次遇到这个节点时路径肯定比第一次加入S时大。
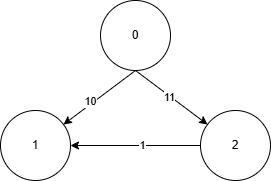
举例上面这幅图,假设从0开始加入集合S,那么下一个加入S的是1,因为10比11小,否则加入的是2。此时0到1的最短路径是10,它还有一条路径是12,可想而知那条路径不可能比10小,即使这副图再加入第三条通往1的路径,也不可能比10小。
✍️ 示例代码
堆优化Dijkstra
dist表示集合S,首先将dist全部置为-1,-1代表未加入到集合S中。当每次遍历到一个cur.i时只要等于-1就将cur.i加入到集合里。然后遍历相邻的节点,计算这个节点到集合S的距离并加入堆中,下次堆会取出最小的距离的节点cur.i。如果只需要找一个点,那么计算到en节点就不需要再算下去了,如果要计算所有节点,参数en传入-1即可。
package main
import (
"bufio"
"container/heap"
"fmt"
"os"
)
type Element struct {
i, w int
}
type hp []Element
func (h hp) Len() int { return len(h) }
func(h hp) Less(i, j int) bool { return h[i].w < h[j].w }
func(h hp) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func(h *hp) Push(x interface{}) {
*h = append(*h, x.(Element))
}
func(h *hp) Pop() interface{} {
n := len(*h)
x := (*h)[n - 1]
*h = (*h)[0:n - 1]
return x
}
func dijkstra(n int, graph [][]Element, st int, en int) []int {
dist := make([]int, n)
for i := 0; i < n; i++ {
dist[i] = -1
}
pq := &hp{}
heap.Init(pq)
heap.Push(pq, Element{0, 0})
for pq.Len() > 0 {
cur := heap.Pop(pq).(Element)
if dist[cur.i] != -1 {
continue
}
dist[cur.i] = cur.w
if cur.i == en {
break
}
for _, nex := range graph[cur.i] {
if dist[nex.i] == -1 {
heap.Push(pq, Element{nex.i, cur.w + nex.w})
}
}
}
return dist
}
func main() {
reader := bufio.NewReader(os.Stdin)
writer := bufio.NewWriter(os.Stdout)
defer writer.Flush()
var n, m int
fmt.Fscan(reader, &n, &m)
graph := make([][]Element, n+1)
for i := 0; i < m; i++ {
var x, y, z int
fmt.Fscan(reader, &x, &y, &z)
graph[x - 1] = append(graph[x - 1], Element{y - 1, z})
}
dist := dijkstra(n, graph, 0, n - 1)
fmt.Fprintln(writer, dist[n - 1])
}#include <iostream>
#include <vector>
#include <queue>
using namespace std;
struct Element {
int i, w;
bool operator > (const Element &other) const {
return w > other.w;
}
};
vector<int> dijkstra(int n, vector<vector<Element>> &graph, int st, int en) {
vector<int> dist(n, -1);
priority_queue<Element, vector<Element>, greater<Element>> pq;
pq.push({st, 0});
while (!pq.empty()) {
Element cur = pq.top();
pq.pop();
if (dist[cur.i] != -1) continue;
dist[cur.i] = cur.w;
if (cur.i == en) break;
for (const auto &nex : graph[cur.i]) {
if (dist[nex.i] == -1) {
pq.push({nex.i, cur.w + nex.w});
}
}
}
return dist;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
vector<vector<Element>> graph(n);
for (int i = 0; i < m; i ++ ) {
int x, y, z;
cin >> x >> y >> z;
graph[x - 1].push_back({y - 1, z});
}
vector<int> dist = dijkstra(n, graph, 0, n - 1);
cout << dist[n - 1] << '\n';
return 0;
}import sys
import heapq
class Element:
def __init__(self, i, w):
self.i = i
self.w = w
def __lt__(self, other):
return self.w < other.w
def dijkstra(n, graph, st, en):
dist = [-1] * n
pq = []
heapq.heappush(pq, Element(st, 0))
while pq:
cur = heapq.heappop(pq)
if dist[cur.i] != -1:
continue
dist[cur.i] = cur.w
if cur.i == en:
break
for nex in graph[cur.i]:
if dist[nex.i] == -1:
heapq.heappush(pq, Element(nex.i, cur.w + nex.w))
return dist
def main():
input = sys.stdin.readline
n, m = map(int, input().split())
graph = [[] for _ in range(n)]
for _ in range(m):
x, y, z = map(int, input().split())
graph[x - 1].append(Element(y - 1, z))
dist = dijkstra(n, graph, 0, n - 1)
print(dist[n - 1])
if __name__ == "__main__":
main()
朴素Dijkstra
朴素写法没有用到堆这个数据结构。朴素Dijkstra的特点是算法复杂度只与图中节点数有关,与边无关,因此非常适合稠密图(边的数量远远大于节点数)。我这次将vis作为集合S,使用邻接矩阵存储图。每次我们做两次节点的遍历,第一次在dist中找到集合S以外最小的节点t,将t加入节点。第二次遍历每个节点,然后在图中查找是否可以从节点t更新到这个节点的dist距离。
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
const int N = 510;
int g[N][N]; // 邻接矩阵
int dist[N]; // 最短距离
bool vis[N]; // 集合S
int n, m;
vector<int> dijkstra(int st, int en) {
vector<int> dist(n, -1);
dist[st] = 0;
for (int i = 0; i < n; i++) {
int t = -1;
for (int j = 0; j < n; j++) {
if (!vis[j] && dist[j] != -1 && (t == -1 || dist[j] < dist[t])) {
t = j;
}
}
if (t == -1 || t == en) break;
vis[t] = true;
for (int j = 0; j < n; j++) {
if (g[t][j] != -1 && (dist[j] == -1 || dist[j] > dist[t] + g[t][j])) {
dist[j] = dist[t] + g[t][j];
}
}
}
return dist;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
memset(vis, false, sizeof vis);
memset(g, -1, sizeof g);
for (int i = 0; i < n; i++)
g[i][i] = 0;
// 处理重边:保留最小的那一条
for (int i = 0; i < m; i++) {
int x, y, z;
cin >> x >> y >> z;
if (g[x - 1][y - 1] == -1 || g[x - 1][y - 1] > z) {
g[x - 1][y - 1] = z;
}
}
vector<int> d = dijkstra(0, n - 1);
cout << d[n - 1] << '\n';
return 0;
}
import sys
def dijkstra(n, g, st, en):
dist = [-1] * n
vis = [False] * n
dist[st] = 0
for _ in range(n):
t = -1
for j in range(n):
if not vis[j] and dist[j] != -1 and (t == -1 or dist[j] < dist[t]):
t = j
if t == -1 or t == en:
break
vis[t] = True
for j in range(n):
if g[t][j] != -1:
if dist[j] == -1 or dist[j] > dist[t] + g[t][j]:
dist[j] = dist[t] + g[t][j]
return dist
def main():
input = sys.stdin.readline
n, m = map(int, input().split())
g = [[-1 for _ in range(n)] for _ in range(n)]
for i in range(n):
g[i][i] = 0
for _ in range(m):
x, y, z = map(int, input().split())
x -= 1
y -= 1
if g[x][y] == -1 or g[x][y] > z:
g[x][y] = z
dist = dijkstra(n, g, 0, n - 1)
print(dist[n - 1])
if __name__ == '__main__':
main()
package main
import (
"bufio"
"fmt"
"os"
)
func dijkstra(n int, g [][]int, st, en int) []int {
dist := make([]int, n)
vis := make([]bool, n)
for i := range dist {
dist[i] = -1
}
dist[st] = 0
for i := 0; i < n; i++ {
t := -1
for j := 0; j < n; j++ {
if !vis[j] && dist[j] != -1 && (t == -1 || dist[j] < dist[t]) {
t = j
}
}
if t == -1 || t == en {
break
}
vis[t] = true
for j := 0; j < n; j++ {
if g[t][j] != -1 && (dist[j] == -1 || dist[j] > dist[t]+g[t][j]) {
dist[j] = dist[t] + g[t][j]
}
}
}
return dist
}
func main() {
reader := bufio.NewReader(os.Stdin)
writer := bufio.NewWriter(os.Stdout)
defer writer.Flush()
var n, m int
fmt.Fscan(reader, &n, &m)
g := make([][]int, n)
for i := 0; i < n; i++ {
g[i] = make([]int, n)
for j := 0; j < n; j++ {
if i == j {
g[i][j] = 0
} else {
g[i][j] = -1
}
}
}
for i := 0; i < m; i++ {
var x, y, z int
fmt.Fscan(reader, &x, &y, &z)
x--
y--
if g[x][y] == -1 || g[x][y] > z {
g[x][y] = z
}
}
dist := dijkstra(n, g, 0, n-1)
fmt.Fprintln(writer, dist[n-1])
}
🧮 时间复杂度
- 朴素实现:,适合稠密图
- 使用优先队列(堆优化):,适合稀疏图
n是节点数,m是边数
🔄 与其他算法对比
| 算法 | 支持负权 | 是否可用于所有最短路径 | 时间复杂度 |
|---|---|---|---|
| Dijkstra | ❌ | 单源最短路径 | (堆优化) |
| Bellman-Ford | ✅ | 单源最短路径 | |
| Floyd-Warshall | ✅ | 任意两点间最短路径 |